CREATION: "Secret Code" map of Math: Mandelbrot set

Monday, May 6, 2024

"Secret Code" map of Math: Mandelbrot set

Fractals: The mapping of Numbers....for infinity

"Did you know that amazing, beautiful shapes have been built into numbers?

Believe it or not, numbers like 1, 2, 3, etc., contain a “secret code”—a hidden beauty embedded within them.
...... a sort of “map.”

In mathematics, the term “set” refers to a group of numbers that have a common property. For example, there is the set of positive numbers (4 and 7 belong to this set; -3 and 0 do not).

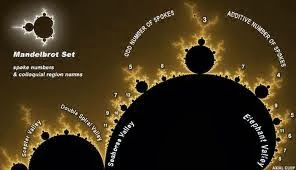
A few decades ago, researchers discovered a very strange and

interesting set called “the Mandelbrot set.”...a “baby” Mandelbrot set is built into the tail of the “parent.”

This new, smaller Mandelbrot set also has a tail containing a miniature version of itself, which has a miniature version of itself, etc.—all the way to infinity.

The Mandelbrot set is called a “fractal” since it has an infinite number of its own shape built into itself.

The formula for the Mandelbrot set is zn+1 = zn2 + c.

In this formula,

---c is the number being evaluated,

---and z is a sequence of numbers (z0, z1, z2, z3…) generated by the formula.

---The first number z0 is set to zero;

---the other numbers will depend on the value of c.

If the sequence of zn stays small (zn ≤ 2 for all n), c is then classified as being part of the Mandelbrot set.

For example, let’s evaluate the point c = 1.

Then the sequence of zn is 0, 1, 2, 5, 26, 677… . Clearly this sequence is not staying small, so the number 1 is not part of the Mandelbrot set.

The complex numbers are also evaluated.

Complex numbers contain a “real” part and an “imaginary” part.

The real part is either positive or negative (or zero), and the imaginary part is the square-root of a negative number.

By convention, the real part of the complex number (RE[c]) is the x-coordinate of the point, and the imaginary part (IM[c]) is the y-coordinate.

So, every complex number is represented as a point on a plane.